Stokes Flow
Square Convection
In this example we compare the numerical predictions of Fluidity with a well-established two-dimensional cartesian geometry benchmark result for Stokes flow (Blankenbach et al., 1989). Fluidity’s results from this, and similar cases, are published in Davies et al. (2011), where solution strategies employed for solving the Stokes system are also discussed.
The specific example considered is steady-state isoviscous convection at a Rayleigh number (Ra) of 105, in a two-dimensional square domain of unit dimensions. Boundary conditions for temperature are T = 0 at the surface, T = 1 at the base, with insulating (homogeneous Neumann) side-walls. For velocity, free-slip and no normal flow boundary conditions are specified at all boundaries.
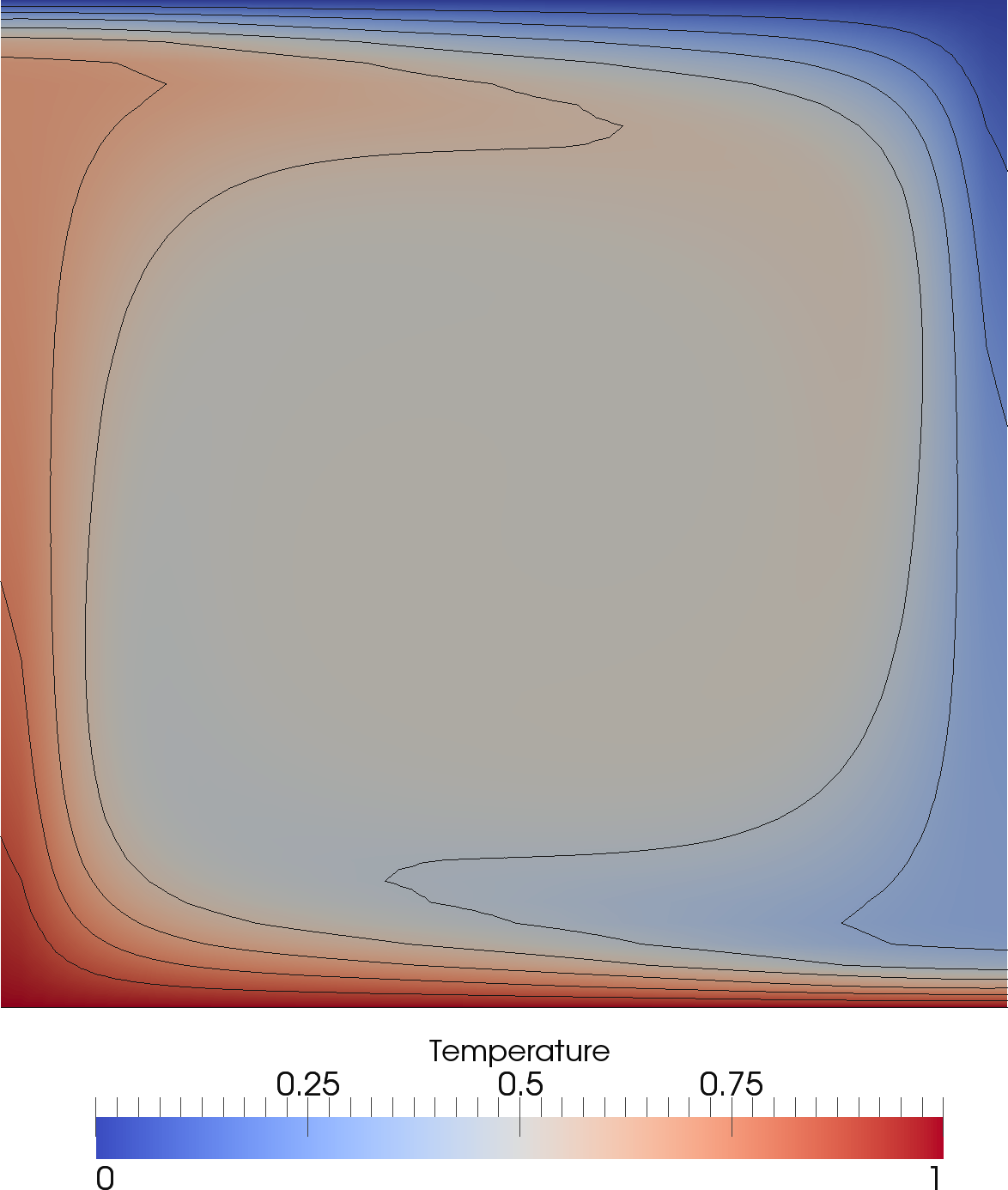
Steady-state temperature field from an isoviscous Stokes simulation at Ra = 105, on a uniform structured mesh of 48 × 48 elements. Contours are spaced at intervals of 0.1.
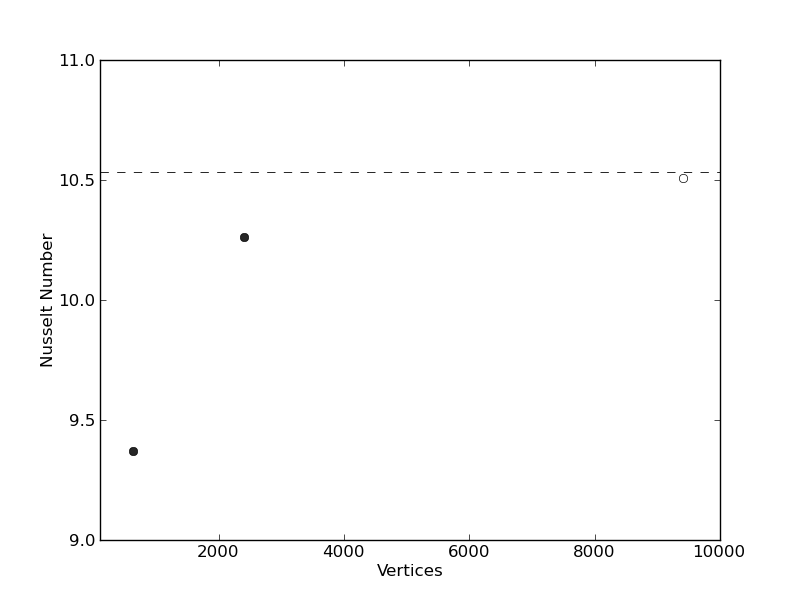
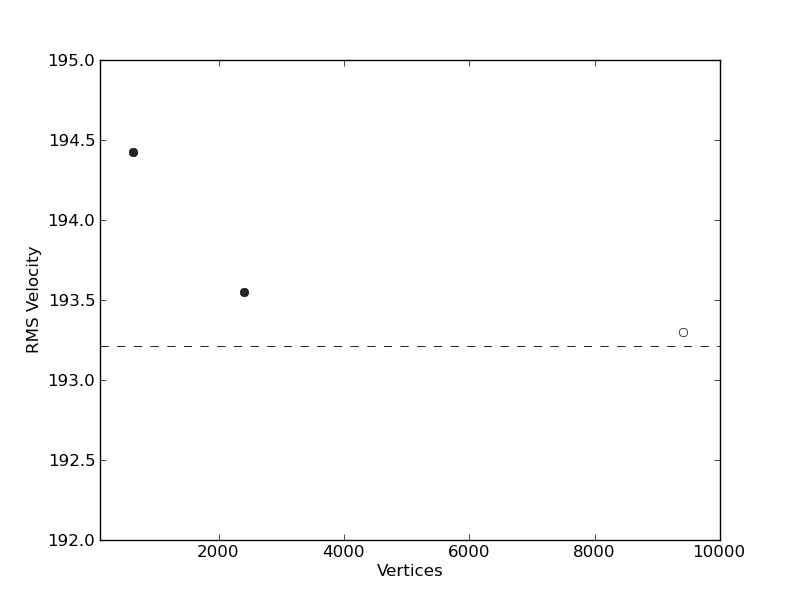
Results from 2-D, isoviscous Stokes square convection benchmark cases: (a) Nusselt number vs. number of triangle vertices, at Ra = 105 [case 1b: Blankenbach et al. (1989), for a series of uniform, structured meshes. Filled circles reporesent the example cases at a resolution of 24 x 24 and 48 x 48 elements respectively. The open circle represents the result from a case at 96 × 96 elements, to illustrate that as mesh resolution is increased, solutions converge towards the benchmark values; (b) RMS velocity vs. number of triangle vertices, at Ra = 105. Benchmark values are denoted by horizontal dashed lines. Note that the highest resolution case is not included in the example.
The results presented in the figures above. The final steady-state solution consists of one convective cell, with hot upwelling flow confined to the left hand side of the domain and cold down-welling flow on the right hand side. Note that, excluding the location of upwelling flow at x = 0 or x = 1, results are insensitive to the initial condition. Quantitatively, results show excellent agreement with the benchmark predictions of Blankenbach et al. (1989), with solution accuracy improving with increased resolution, as expected. A higher resolution case (at a resolution of 96 × 96 elements), achieves results that are almost identical to the benchmark solution.
References
Further details about Fluidity's Stokes flow model can be found in the following paper:
- D. R. Davies, C. R. Wilson, and S. C. Kramer. Fluidity: A fully unstructured anisotropic adaptive mesh computational modelling framework for geodynamics. Geochem. Geophys. Geosyst., 12:Q06001, 2011. doi:10.1029/2011GC003551